The Combinator Calculus

The Combinator Calculus/SKI Calculus, introduced by Schonfinkel and Curry, eliminates the need for quantified variables in mathematics.

I x -> x : Identity function

K x y -> x : Constant functions

S x y z-> (x z) (y z) : Generalised function application

supporting multiple Arguments

K : A function by itself is a well-formed program, no rules apply.

K x : No rules apply to K with one arg

K x y -> x : K only executes with 2 args

K x y z -> x z : K only uses the first two args

The terms of the SKI calculus are the smallest set such that S, K, I are terms, and if x and y are terms, then x y is a term. Terms are trees. 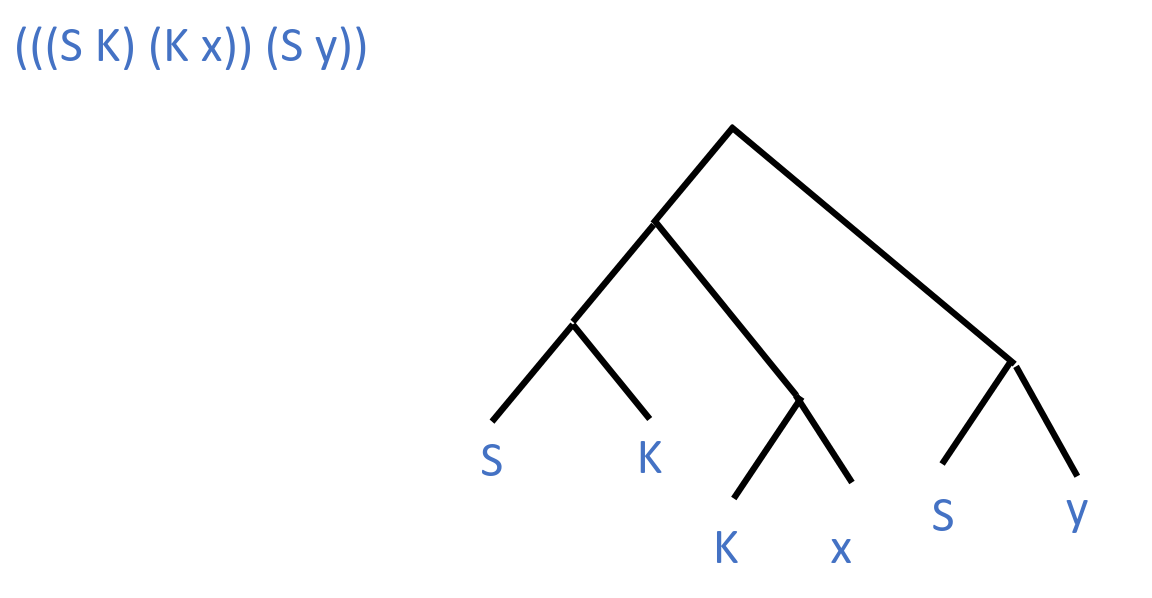Context-free grammar 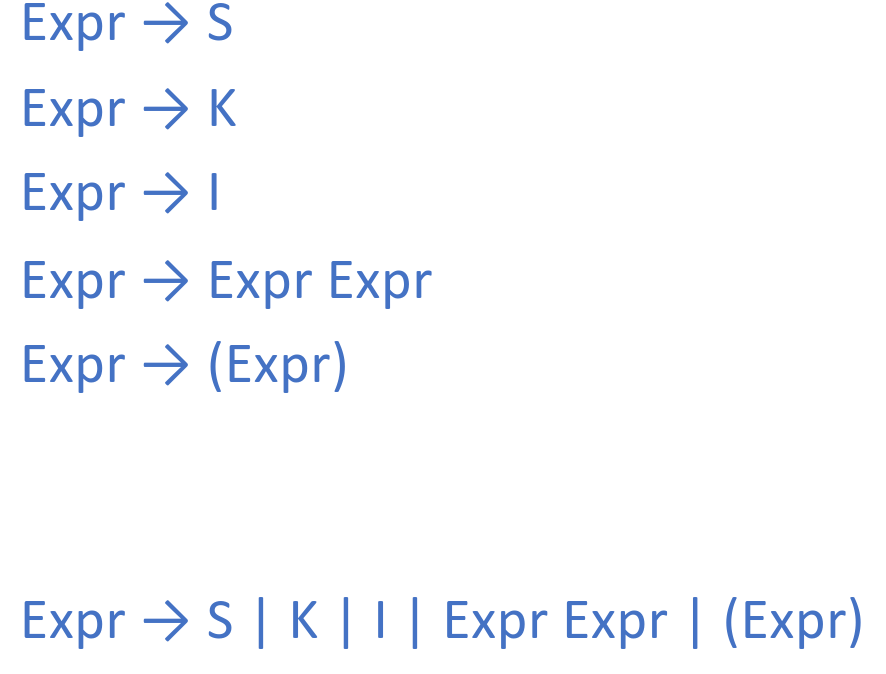It is similar to Lambda Calculus, but without the concept of closures, meaning it avoids the issue of opaque closures at the cost of not being able to form abstractions at all and having to encode combinators as rewrites. One famous example of a programming language based on the Combinator Calculus is

>>> Nock